Sean Lynn McKell, Department of Electrical and Computer Engineering
Overview
A little-known phenomenon recently explored by a few engineers seems, to some, to be a little out of focus. This phenomenon, dubbed “fuzzy logic” by its inventor, Lotfi A. Zadeh, is an oxymoron to mostit connotes something ethereal and misplaced in a field such as engineering which demands precision in order to produce results which work and do something useful. This “fuzzy” thinking, as an engineer might say, should instead be found in the circles of those humanists who often are immersed in endless debates about whether life is real or not.
Zadeh gave birth to the term fuzzy logic with a paper he published in 1965 entitled “Fuzzy Sets,” [1] In an interview, he noted that two-valued, yes-orno logic has sharply defined boundaries. But, this is too precise for much of common sense human reasoning and is too confining [2, pp. 15-16]. For example, think of trying to describe every condition which leads a defensive basketball player to jump at the correct time to block a shot-he/she doesn’t measure that an opposing player started to shoot .z seconds ago and that they must jump 21.5 inches in order to block the shot. Instead, the player thinks to himself, “the opposing player just started a jump to shoot, so I must jump now and jump high.” These imprecise words describe in good enough detail what the player must do in order to accomplish his purpose of blocking the shot.
In many mechanisms in the world, electronic hardware and software are used to control processes associated with them. The implementations of these controllers are varied, with many of their designs employing exact algorithms. But, this exactness can pose problems for the controlling systems because of excessive and overly-precise responses which can cause jerkiness and overshoot. Also, models of the control system might not be exactly implementable in practice, because the controller may be excessively strained and would breakdown under certain conditions. Fuzzy logic applied to control, though, can possibly solve these very problems of jerkiness and overshoot particularly because it isn’t excessive and overly-precise; and, with respect to models, this imprecision helps it to be robust over a variety of conditions. So, in this project, fuzzy logic control was used to balance an inverted pendulum straight up, like keeping a rocket pointed upwards.
Concept of Fuzzy
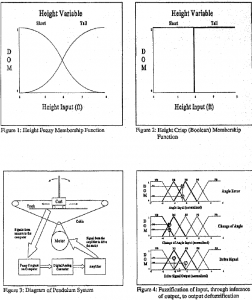
To illustrate fuzziness, and define some seminal terms in the area, consider Figure I: here is shown a fuzzy variable, Height, and its membership function. A membership function consists of an input range and fuzzy sets which have a defined degree ofmembership(DOM) for every value of the input range. The membership function for this Height variable shows a Short and a Tall fuzzy set with their DOMs graphically defined. To use this function, let’s say someone is 5.5 ft high. We go to the Height input of 5.5, draw a perpendicular line straight up from it, and find that this person is Short to the degree of about . 7, and Tall to the degree of about .3. So, if we wanted to qualify this person linguistically according to the function defined, this person would be more short than tall, but has elements of both. The fuzzy sets here were specified intuitively by the author, but could also be influenced by statistical data.
The ability to have both one trait and aspects of an opposite trait is a distinguishing characteristic of fuzzy logic in comparison to boolean, or bivalent, logic. Boolean logic excludes the notion of an object being both; instead, an object can only be defined or described as having one trait or another, it can’t be a bit of both. Figure 2 shows what happens to the height variable using boolean logic. Here we see that for any input value, that value must either fall into the Short set, or the Tall set with DOM of I. Since there is no fuzziness about what set an input maps to, these sets are called crisp.
Thus we see that the boundary between height descriptions for a fuzzy variable is imprecise, vague, or (to be redundant) fuzzy, while the boundary between descriptions for a boolean variable is precise, hard-fast, or sharp.
Fuzzy and the Inverted Pendulum
Figure 3 shows a diagram of the pendulum system, including the cart and electronics used to control it. A computer program implement ing fuzzy logic was created to perform the control of the system. A simple description of fuzzy logic control as implemented by the program follows.
The most basic inputs to the program are the angle and change of angle of the pendulum. These inputs from sensors are fuzziiied into a fuzzy variable as shown in Figure 4. The scale on the bottom of the membership functions’ graphs is a scale normalized to max and min angle settings. For example, if the angle error input (normalized) is -.5 (as shown), then the angle is considered to be .75 ZEro and .25 NegSmall. Using linguistics and logical thinking, we make up a rule set in an “IF this AND this, THEN that” fashion. For the example shown, we would logically induce, for one rule, that “IF (angle is NS) AND (change of angle is NegBig), THEN (drive output is N egBig)” in order to keep the pendulum balanced. A collection of these rules to cover the possibilities of inputs is compiled into the rule set, and thus control can theoretically be achieved.
The DOMs are used ultimately to find the correct output value for the drive signal. As seen in Figure 4, and by using the rule set, the various inputs with their DOMs give two output fuzzy sets for the Drive Signal, with a DOM corresponding to each fuzzy set. The output fuzzy sets along with their DOMs come from a process of max-min composition of the combinations of inputs and how they map to outputs. After ANDing (taking the minimum DOM) two input fuzzy sets, the resulting minimum DOM is assigned to the corresponding output fuzzy set; this is performed for all four possibilities. After all the possibilities are gathered, the output fuzzy sets with the maximum DOMs (in Figure 4’s case, NS of degree .583 and ZE of degree .333) are used to obtain an output value. This output value is the “center-of-gravity” between two sticks placed at the center of the pertinent fuzzy sets, and of weight equal to the DOM corresponding to the fuzzy sets. In Figure 4, we see that the output is- 1.27 for the case shown. This output value is the defuzzifled output value, and will be de-normalized to a value useful for the particular pendulum system signal which will be sent to the motor to drive the cart in such a way as to balance the pendulum.
Results and Conclusion
In actual tests, this fuzzy logic control system was able to balance a pendulum for about 10 seconds. Another system, built by Yamakawa [3], was apparently more successful in balancing for a longer period of time. But, the advantage of fuzzy logic became clear: it is a more intuitive, straight-forward method of controller design than other conventional methods. Instead of a complicated math equation, heuristic rules were applied to obtain control of the system. With more adjustments to the fuzzy sets in the variables (“tuning”), better control of my system could hopefully be achieved.
For now, fuzzy logic is an elegant way of approaching certain problems, but it is still not as accepted as the more precise, mathematical, conventional approaches. Its merits, though, have prompted progressive practitioners, mainly Japanese, to incorporate the technology in various products, including washing machines, video cameras, anti-lock brakes, automatic train systems, heater/air conditioners, and more. Combined with neural networks, Kosko [5] believes that fuzzy logic can reach its full potential in machine intelligence, taking us one step further on the way to greater automation in our world.
References
- Zadeh, L.A., “Fuzzy Sets,” Information and Control, Vol. 8, 1965, pp. 338-353.
- Yager, R.R., Ovhchinnikov, S., Tong, R.M., Nguyen, H.T. (Eds.) Fuzzy sets and applications: Selected papers by LA. Zadeh. New York: Wiley, 1987.
- Yamakawa, T., “Stabilization of an Inverted Pendulum by a High-Speed Fuzzy Logic Controller Hardware System,” Fuzzy Sets and Systems, Vol. 32, 1989, pp.161-180.
- Kosko, B., Fuzzy Thinking: the New Science of Fuzzy Logic. New York, NY: Hyperion, 1993.