Michael Jones, Department of Computer Science

As computer systems become an integral part of society, ensuring that systems perform correctly will become more important. Proofs of correctness based on formal logic are one approach to the correctness problem in computer system design. Unfortunately, these proofs are often large and difficult for industrial size projects. The Higher-Order Logic (HOL) [GM93) automated proof assistant helps manage the details and validate the accuracy of large proofs.

A particularly common type of proof in computer system design involves demonstrating that a given boolean function is true for all combinations of inputs-such a function is called a tautology. Computer systems can be easily represented as boolean functions. However, the size of tautology proofs grows exponentially with the number of variables, quickly becoming intractable even for reasonable functions. By using binary decision diagrams (BDD) [Bry86) to represent and reason about boolean functions, more tautology proofs are made tractable.

In this project, we build on the work of John Harrison [Har94) to create a BDD based tautology checker for the HOL system. Harrison’s BDD based checker is built inside the HOL logic using HOL’s primitive axioms and inference rules to create a sound framework in which to use BDDS. This approach creates a checker that is both reliable and slow. Our BDD based checker is built outside the logic using the HOL’s meta-language (called ML) and results are surreptitiously made into theorems and injected into the logic. We’d hoped our approach would be both unreliable and fast. Instead, we’ve managed to create a BDD based tautology checker ‘written in ML that is both less reliable and slower than Harrison’s derived rule implementation.

Implementation

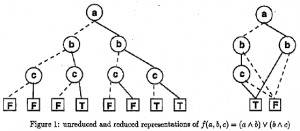
The graphs in figure 1 depict two BDD representations for the threevariable boolean equation f (a, b, c)= (a A b) V (b A c). Each node (circle) of the graphs is labeled and represents a variable in the function. The edges (lines) connecting the nodes represent the variable’s particular value. Dotted lines represent the value F, or false, and solid lines represent the value T or true. The boxes at the bottom contain the value of the equation for a given path through the graph.

For example, to find the value off (I’, F, T) (using the unreduced BDD on the left) we work our way down the tree using the values of the variables as a guide in picking the correct path. Since a is true we descend its right edge to b. Next, we descend b’s left (false) edge and finally we choose to go right from c. Upon reaching a final node (box), we find that f(I’, F, T) =F.

Careful observation of the unreduced BDD reveals that in contains extra information. For example, if b is false the f (a, b, c) is also false regardless of the value of c. A host of rules have been developed to reduce BDD representations of boolean equations [Bry86) . The reduced version of the BDD for f (a, b, c) = (a A b) V (b A c) appears on the right side of the figure and is much smaller and requires fewer decisions to evaluate f. If we re-evaluation off (I’, F, T) using the reduced graph, we can reach a final value in two steps rather than three.

Building the reduced BDDs to check for tautology is by far the most expensive part of BDD based tautology checking. Once the BDD is built checking for tautology is relatively simple and fast. Our method for constructing BDDs in ML parallels the one presented by Harrison [Har94]. To construct the reduced BDD for a given equation, we first make BDDs for each of its variables then recursively combine them into subexpressions and combine the subexpressions into larger expressions until the entire function is represented. After each combine operation the resulting BDD is reduced before being combined again. By doing so, we reduce the BDD as we build it rather than making one big reduction upon completion.

Two optimizations are used to make BDD construction more efficient. First, a table of previously computed results is kept to prevent repeated work. Before the BDD for a subexpression or variable is created the table is checked. If the expression appears In the table, further computation avoided by using the BDD in the table. If the expression does not appear, the BDD is created and stored in the table. The second optimization involves negating adjacent computation avoided by using the BDD in the table. If the expression does not appear, the BDD is created and stored in the table. The second optimization involves negating adjacent edges rather than descendant nodes to represent a negated variable. Thus making negations virtually free by eliminating the need to change more than a local edge.

However, due to the nature of the ML environment, our implementation could make only limited use of the lookup table. To take full advantage of the table requires the ability to create and use arrays in a constant-time search algorithm. ML is a functional language and does not have the facilities for doing so. In our implementation, we approximated a lookup table using a fairly convoluted data structure based on Paulson’s functional arrays [Pau91].

Results from checking the BDD for tautology are used in two ways. If the represented function is not a tautology, the BDD checker returns a counter example for which the function is false. If the ML checker determines that the function is indeed a tautology, a call to mk-thm makes the function into a theorem in the logic. Using mk-thm is unsafe, but is the price we pay to define our BDD based test outside of the logic.

Results and Further Work

The goal of an ML implementation of BDDs in HOL was to sacrifice proof security for speed, thereby creating a kind of “rough draft” method for checking large boolean expressions for tautology. The implementation was moderately successfuL For small expressions, the ML function performed comparably to Harrison’s derived rule implementation. Unfortunately, for large expressions, the ML function was significantly slower than the derived rule. Code analysis indicates that the problem is the lookup table. By using an array based table, Harrison’s BDD tactic enjoys a constant time search function. The functional array approximation of a table implemented in ML did not provide a sufficiently fast lookup function especially when results became large.

Table 1 summarizes comparative times for the ML implementation and the derived rule. The benchmark files are found in [VC90) and results for the derived rule implementation are taken from Harrison [Har94). Completion times for the derived rule rise at an almost reasonable rate while completion times for the ML implementation increased rapidly before consuming 128 Megabytes of internal memory and failing.

Future work will focus on improving the both the behavior and representation of the lookup table. Also, the matching rules and hashing function for the lookup table will be improved. For example, terms which are not identical, but equivalent (through commutivlty for example) should match. A better approximation of a hashing function would also improve performance.

References

• Randal E. Bryant. “Graph-Based Algorithms for Boolean Function Manipulation.” IEEE Transactions on Computers. 1986. C-35:677 -691.
• Gordon, M.J,C., and T.F. Melham. Introduction to HOL: A Theorem Proving Environment for Higher Order Logic. Cambridge Univeristy Press, 1993.
• John Harrison. “Binary Decision Diagrams as a HOL Derived Rule.” Higher Order Logic Theorem Proving and Its Applications. 1994. 254-268.
• Larry Paulson. ML for the Working Programmer. Cambridge University Press, 1991.
• Diederek Verkest and Luc Claesen. “Special Benchmrk Session on Tautology Checking. In Formal VLSI Correctness Verification. Elsevier Science Puclishers, 1990. 81-82.