JJ Campbell and Dr. David Neilsen, Physics
Chaos. Some say that this word describes the world today. From the point of view of physics, they would be right. If we take “chaos” to mean an extreme sensitivity to initial conditions with exponentially diverging solutions then this world is chaotic on a number of levels, all the way from the structure of bacterial growth in a natural environment to how the solar system interacts, we are stuck in the middle of chaos. Understanding just how small changes affect the future would be very useful. Imagine what could be done if we knew exactly how a disease would spread, where to expect droughts next year, when the market will make the next historic drop, or what the chances really are of an asteroid impacting Earth.
As soon as we start talking about celestial bodies we also need to start looking into Relativity. There are two main categories of Relativity, General and Special. Special Relativity deals with motion and the idea that the speed of light is constant. Special Relativity is usually only taken into account when things are moving really fast. In this study we do not move that fast until things become too unrealistic to matter. General Relativity, on the other hand, deals with the concept that our 4D space-time is not “flat”. In other words, the shortest distance between two points is not really a straight line. To get some grasp of this, imagine being stuck to the surface of smooth Earth. Without digging, the shortest piece of string that can be used to connect any two points on this earth is the shortest possible distance. On Earth this string will look like a straight line. From the perspective of the man who conveniently standing on the moon, this string curves. This example is the 2D equivalent of space-time as seen through General Relativity.
The three-body problem elegantly combines both Chaos and Relativity. A two-body problem, such as a binary star, or the earth and moon, is solvable. Equations can be derived to tell where both of the objects will be at any given time. The three-body problem is not quite that simple. The equations become non-linear differential equations when we get to three bodies. In English, this means it is not worth trying to do much with them unless you are using a computer. With modern computers we are still not able to solve the equations, but we are able to simulate the motions for given beginning parameters. Since chaos is defined by an extreme sensitivity to initial conditions, and exponential divergence, this means that if I change something I need to run another simulation.
Let us say I am using three small stars. In the first simulation star 2 gets thrown out of the system and stars 1 and 3 become a binary. If I were to hit number 3, lets say with a baseball bat, it is possible that my bat will change the outcome such that star 2 now gets ejected. This may seem a bit extreme considering the relative sizes, but that is the whole point.
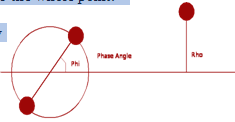
My research has been done by creating a theoretical binary star system and then throwing another star in from infinity. The stars on the left in this picture represent the binary, and the one on the right is the third object. We have constrained the motion to the XY-plane by starting everything with zero position and momentum in the Z direction. By varying Rho and Phi by tiny amounts and then running thousands of simulations on the supercomputer MaryLou4 we have mapped this system using Newtonian physics. We measure only frame independent variables, such as which body escapes, and then use a 3D graph to record the Rho, Phi, and the other variable for each simulation. By making the colors represent the Z-axis of the graph we can easily see which body escaped for any given value of Rho and Phi. This graph covers Phi from 0 to 2*Pi on the X-axis, and the Y-axis runs from where the incoming body misses the binary completely both “above” and “below” the binary. The orange and green each represent one of the two stars in the binary, and as we pass Pi we see that the two simply switch places. The red represents the incoming body. The dark blue is where the stars passed too closely to one another and killed the program. The speckled areas are where you see the chaos. With each pixel on the graph being a separate simulation, we can see that infinitesimal changes really can have a great effect.
This was already known though. The interesting part comes when we apply the Post-Newtonian corrections to the Newtonian model. We run corrections to the Newtonian model instead of the full General Relativistic equations because one or two simulations would take longer than the thousands you see to the left. The Post-Newtonian corrections give us a way get progressively better simulations without nearly as much computational time. The corrections are very small, but with chaos even the smallest of changes starts things moving.
The picture on the below is a perfect example. This second graph shows the first order Post-Newtonian correction run with the exact same parameters as the one above. Some basic shapes and designs have remained, but particularly around the areas of close encounters in the Newtonian model (dark blue) we now see “rivers” of Chaos forming.
The future studies that can be done here are vast. We have started zooming in on areas to focus on the fine structure, or the rivers of order that flow through the regions of chaos. We have begun varying one or more of the masses. We removed the XY-plane constraint thereby creating some fascinating graphs. The next big thing though, is to extend the research to include the next orders of correction.
