Kyle Matt and Denise Stephens, Department of Physics and Astronomy Department
The purpose of this project was to improve upon a method for discovering binary brown dwarf systems, and create a program to speed up the implementation of that method. A Brown Dwarf (BD) is a celestial object that is not massive enough to undergo hydrogen fusion in its core, meaning it is too small to be a star, but is also too big to be a planet. BDs can form in low-mass binary pairs. A stellar object located many parsecs away will act as a point source of light for an observer on Earth, therefore the light from such an object will spread out from a central point in a predictable pattern known as its Point Spread Function (PSF). Due to the great distances between Earth and these BDs compared to their separation, their two respective PSFs will overlap to some degree and the binary system appears to be a single, unresolved object in telescope images. Figure 1 shows this process, if the PSFs have a separation less than what is known as the Rayleigh limit, they form a single PSF that cannot be resolved into two.
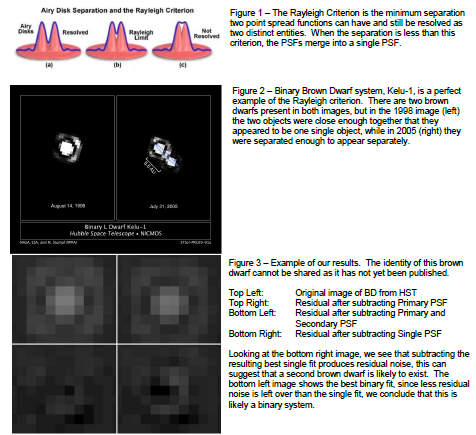
Kelu-1 is a known binary BD system that demonstrates this phenomenon well. Its highly elliptical orbit brings the two BDs near each other (1.15au) and also far apart (11.65au). This contrast allows us to see them both resolved and unresolved. In Figure 2, if one were to only look at the 1998 image, they might conclude that it was a single object, while the 2005 image clearly depicts two distinct BDs.
In 2006, my advisor, Dr. Denise Stephens, and an associate, Dr. Keith Noll, developed a method using model PSFs to identify binary Trans-Neptunian Objects. This method works by comparing model PSFs of single and binary sources to the observed PSFs, subtracting the model from the observed data and examining the residuals to determine the probability that the system is a binary. We have modified this method to identify binary BD systems in the Hubble Space Telescope archive.
The model PSFs we use are produced by the TinyTim software developed by Krist & Hook in 2003 and are unique to each camera, filter and spectral type (type of brown dwarf). The PSF produced is subsampled by a factor of 10 to produce a PSF 10 times as wide and tall as that of the image. This is then rebinned by 10, shifting the PSF by one pixel at a time to produce 100 model PSFs that each vary the center by 0.1 pixel in both x and y.
I wrote a program that will iteratively test each model PSF to find a best fit for first a single object, and then a binary system. This is done by subtracting each model PSF from the actual data and comparing the residual noise. Then the program takes two PSFs and iteratively combines them by varying the center and brightness of each PSF. This combined PSF is compared to the actual data in the same way as the single fit and residuals are compared. We determine which model is most correct by performing a chi-squared test, a common statistical method to determine how probable a result is to be due to chance. We accept results when we find the binary fit with a value three sigma greater than the single fit, this means a less than 0.3% chance of our findings being a false positive.
The program returns the best binary PSF results, and these can be used to determine the angular separation, orientation, and relative brightness of the two objects. We can then scale each model PSF by the appropriate brightness from the fit and calculate magnitudes for the primary and secondary object in each filter.
Figure 3 shows some of our results, this is four images of a suspected binary brown dwarf system that we have been studying. The identity of this system cannot be revealed here as it is not yet published.
Thus, using the Model Point Spread Functions of both single and binary Brown Dwarf systems, it is possible to identify unresolved binaries and find their respective brightness and separation. This technique can be used with data in the Hubble Space Telescope’s archive to identify binary brown dwarf systems that were previously unknown. This will provide more candidates for future binary studies and provide separations that could be used in the future to constrain orbital solutions.