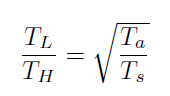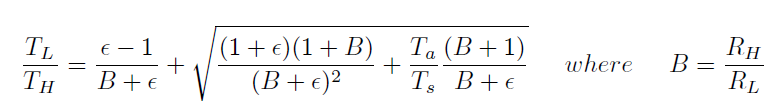Zachary Sadler and Faculty Mentor: Matthew Jones, Mechanical Engineering
Introduction
Energy is an important resource within the world we live. The demand for power requires new energy resources. Much of the power that is generated is eventually wasted in the form of waste heat. As much as 435 GW of energy is transferred from virtually all energy conversion devices and processes to the atmosphere as wasted heat [1]. Converting as much as one percent of this waste heat into electrical power would eliminate the need for 18 average size (236 MW) [2] coal red power plants. A significant portion of this waste heat production is due to air compression systems – a process which converts 60-90% of input power to waste heat [3]. Thermoelectric generators (TEG) are solid state direct energy conversion devices that have the ability to reclaim this otherwise wasted heat by converting thermal energy into electrical energy. While current TEGs have low energy conversion efficiencies, a significant amount of power can be produced with proper optimization. For this project, a model was created and confirmed with experimental data. Creating an accurate model requires taking into account the many external variables which affect the system. With a proper model, professionals will be able to optimize and implement the TEG systems on a broader scale.
Methodology
A model was created by expanding the definition of heat flux [4]. Additionally, the Carnot efficiency and device heat conversion efficiency were taken into account to get the expected power output [5]. These can be seen in equation 1.
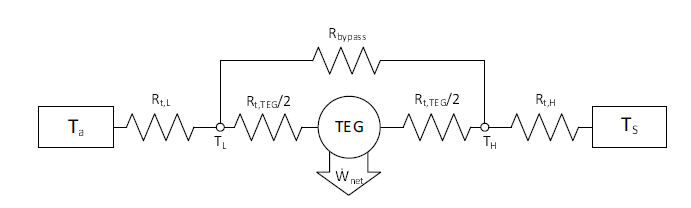
The model created for this project outlines the thermal pathways as shown in figure 1. Ta is the ambient temperature while TS is the source temperature.
Figure 1: Thermal Resistance Diagram
The thermal pathway diagram allows for thermal energy to bypass the TEG. This would be sources such as conduction through insulation, convection or radiation. Only considering the thermal energy that goes through the TEG and adding an expression for device efficiency [6] yields the complete model which can be seen in equation 2.
A further relationship between the various temperatures in the for a reversible process for the maximum heat transfer (Equation 3).
A more precise relationship was derived for real, non-reversible processes:
In either equation (equation 3 or 4), changing the temperatures requires changing the contact resistances, Rt,H and Rt,L, between the TEG and source/heat sink.
The model was verified with experimental data. The maximum measured temperatures on the surface of the air compressor was found to be 200 °C. An experiment was run with a hot plate keeping the hot side of the TEG at 200 °C while a heat sink cools the cool side. Additionally, contact resistance and electrical load resistance are varied to show the importance of optimizing the system.
Results
According the model, maximum power will be generated by the TEG when TH is as high as possible and TL is as low as possible. This would be when TH = Ts and TL = Ta. This can be seen in equation 1. This neglects the need for heat transfer through from the source to the hot side of the TEG and from the cold side of the TEG to ambient. If TH = Ts and TL = Ta, then no heat transfer would occur through the system. This heat transfer rate is governed by the contact resistance between the heat sink/source and the respective sides of the TEG. The contact resistance should be chosen so that it follows equation 3.
Experimental Data from one test yielded Ta = 20 °C, TL = 57 °C, TH = 139 °C and Ts = 201 °C. The experiment generated about 1.8 Watts from the TEG. The current implementation of the model yields about 1.2 Watts. The model is not quite as accurate as preferred but the research will be continued to get the model and experiment data are within the range of uncertainty. It must be noted that the bypass heat transfer was neglected for the model at the current state in order to reduce the number of places for error to be introduced by estimates. Many of the parameters such as thermal resistance and figure of merit must be estimated because they change with temperature.
Discussion
Currently, the model and the experimental data differ slightly. There could be several different reasons why the model and experiment disagree. One obvious place for there to be error introduced is neglecting the bypass heat transfer.
One thing that was noticed in this experiment was that the model depends upon knowing not only the source and the ambient temperatures but also the TEG surface temperatures. The temperature of the hot and cold sides of the TEG can be difficult to get, even in a lab setting. It is not realistic for a professional to be able to get these temperatures. These temperatures should be replaced with other parameters.
Additionally, the figure of merit of a TEG (Z) is a difficult number to obtain as it requires specialized equipment. A reliable means of obtaining this number would help to simplify the calculations for this model.
Conclusion
While the model is not yet finished, the results are promising that the amount of power from a TEG can be predicted and allow for optimization. More work is needed to refine the model as well as simplifying the model. With this model, thermoelectric generator power harvesting systems offer a promising method of partially meeting the world’s demands for power by allowing for more efficient use of the power that has already been generated.
References
- U.S. Department of Energy, 2008. “Waste Heat Recovery: Technology and Opportunities in U.S. Industry”. p. 112.
- U.S. Energy Information Administration, 2014. 2014 form eia-860 data – schedule 3, ‘generator data’ (operable coal units only).
- Cerci, Y., Cengel, Y. A., and Turner, R. H., 1995. “Reducing the Cost of Compressed Air in Industrial Facilities”. Thermodynamics and the design, analysis, and the improvement of energy systems, 35, pp. 175-186.
- Bergman, T. L., Lavine, A. S., Incropera, F. P., and Dewitt, D. P., 2011. Fundamentals of Heat and Mass Transfer. John Wiley & Sons, Inc.
- Cengel, Y., and Boles, M., 2010. Thermodynamics: An Engineering Approach, 7th ed. McGraw Hill.
- Lee, H., 2010. Thermal Design. John Wiley & Sons, Inc.