Brett Rowberry and Dr. Larry Howell, Mechanical Engineering
Normal and right-angled n=6 kaleidocycles are structures composed of six tetrahedra. They are capable of continuous rotation while only requiring 240° of rotation on each joint between adjacent tetrahedra. Because of this fact, kaleidocycles may be made fully compliant with no moving parts. Having continuous rotation in a monolithic fully compliant structure is rare, if not unique. One consequence of having compliant joints is that as they are flexed from their unstrained positions, energy is stored. As the kaleidocycle is rotated, energy is stored and released from each of the joints in a complex manner. The purpose of this research is to investigate and quantify the stable states resulting from various arrangements of joints with differing stiffness and unstrained positions.
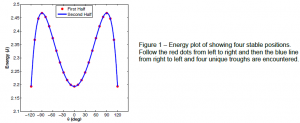
Because three-dimensional modeling and tracking of six individual joints is highly difficult, some assumptions were made. Firstly, it was assumed that although there are six joints, they are of only two types. Secondly, all joints of the same type undergo the same angular deflection and in a synchronous way. Thirdly, the deflection of all the joints can be related to a single variable – the angular deflection of a single joint. Fourthly, all the joints of a single type have the same stiffness and unstrained position. Fifthly, the stiffness of the joints was assumed to be linear. With these assumptions in place, the energy across any given joint, and for the whole structure, can be related to the angular displacement of an arbitrary joint. Plots were obtained showing energy versus angular displacement for an exhaustive eleven cases. Stable states are defined as points of minimum energy. The analytical model was qualitatively validated by a physical model, which exhibited the same behavior.
As a result of the analysis, it was determined that stable states do indeed occur when the summation of strain energy in the two types of joints is at a minimum. When the difference between the stiffness of two different types of joints is large, the kaleidocycle behaves as if there is only one joint-type present. As the conditions in one of the eleven cases approach the conditions in other cases, the behavior becomes less clearly defined. Of the eleven cases, two are quadstable, two are bistable, and seven are monostable. Sharp stable equilibrium positions lead to interesting behavior where unstable states are highly unlikely to occur, a generally desirable behavior for switches and similar applications. Another interesting case had the property of neutral stability for some portions of motion, implying that large motions could be obtained with little energy input. Another interesting feature is that some cases exhibited asymmetry, giving pathdependent behavior.
Future work on the mathematical model could address the assumption of linear stiffness. In addition, equations could be developed for evaluating the magnitude and angular position of the stable states by making use of gradient concepts. Also, equations relating the angle of rotation of the whole kaleidocycle, to the input angle of rotation on a joint, could be developed. The physical model could be instrumented for measurement of moment across the torsional springs and joint angles.